閉鎖空間を考える
次の例を見てください。
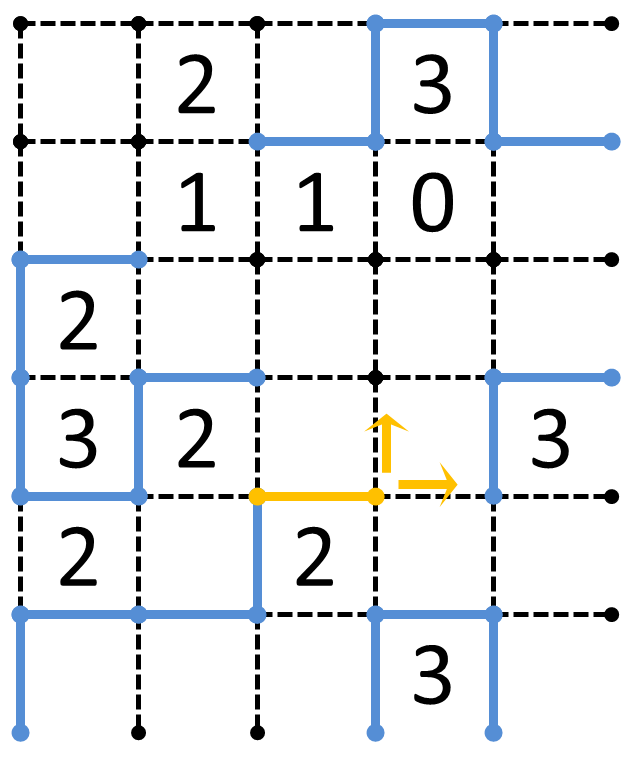
「左上から解いていけ!」というツッコミは無しとして、ここでは上図のオレンジ色の線分を右に延ばすか上に延ばすかを考えたいと思います。
今回は試しに右に延ばしてみましょう。すると下図のようになります。
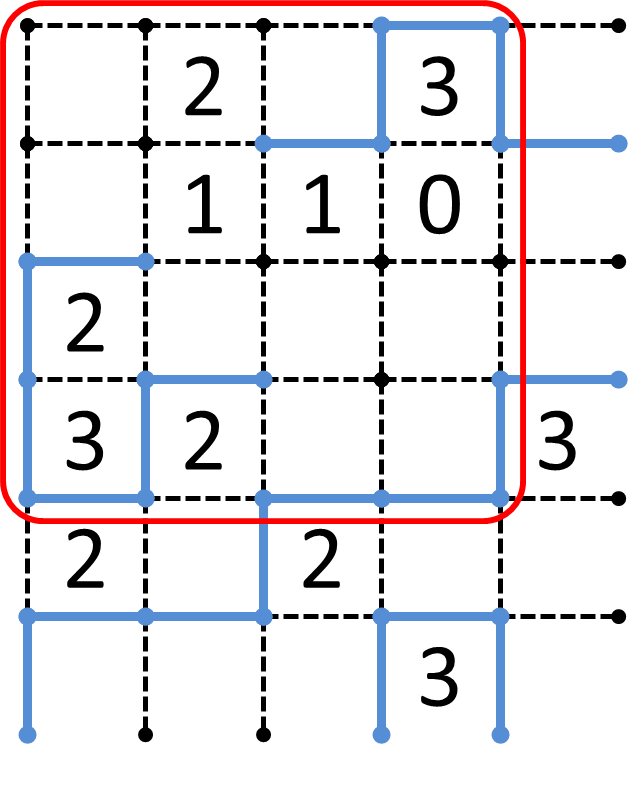
ここで、赤枠で囲んだ部分は、もうこれ以上どこかから線分の一端が侵入してくることはありません。ここでは、これを便宜上、閉鎖空間と呼びましょう。
さて、それを踏まえた上でこの閉鎖空間を見てみると、この閉鎖空間内では、線分の端部が3つしかないことに気づくと思います。
最終的にひとつの輪を構成する必要があるのに、これでは3つのうちどれか1つが輪を作れずに余ってしまいます。
そこで、先程のオレンジ色の線分を右ではなく、今度は上に延ばしてみましょう。
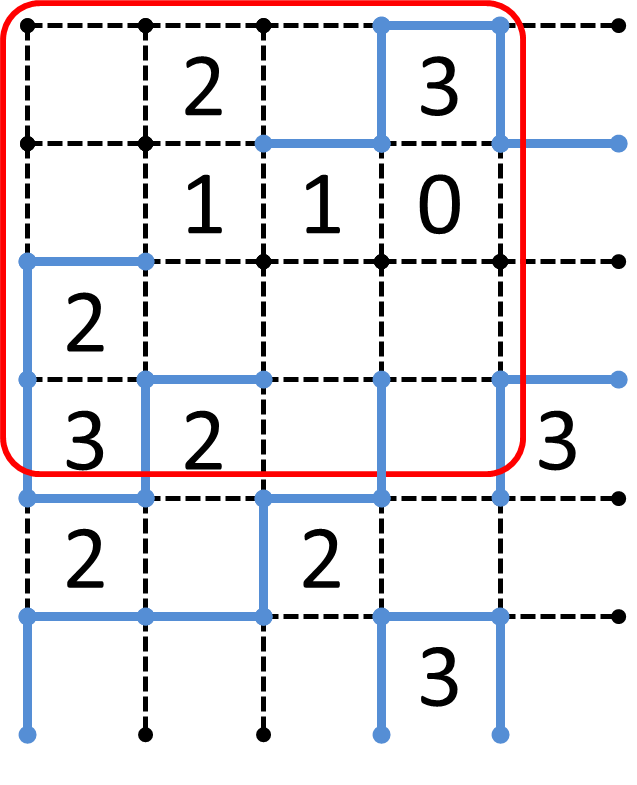
これなら閉鎖空間内に4つの端部があり、最終的に余ることがなくなるのが分かると思います。
以上のように、問題を解いている過程で、その一手によって空間が閉鎖され、空間内の線分の端部の数が決まる場合があります。
この場合、閉鎖空間内の線分の端部の数が偶数となるように線を引いていきましょう。
上で挙げた例は比較的シンプルでしたが、閉鎖空間が確定する状況であれば、端部の数が10個とか12個でも応用できる方法です。
手詰まりと思ったときは、全体を俯瞰して見てみると閉鎖空間の可能性に気づくこともあるかもしれません。