ついにモザイクアート攻略法・上級編に突入です。
ここの内容を理解するには、少なくともモザイクアート攻略のコツ~中級実践編②~を理解している必要があります。
検索で直接このページに来られた方は、まずそちらからご覧ください。よろしくお願いいたします。
1列に並んだ数字に着目する
モザイクアートでは、1列に並んだ数字というのが特に手がかりになりやすいです。
それは、端から1列3マスずつで区切っていき、順々に黒マスが入る数を予測していく中で、そのうち「全部黒マス」「全部空白」の列に突き当たれば、そこが確定できるから。
…と言葉で説明してもよく分からないので、百聞は一見にしかずということで早速実例を見ていきましょう。
例1

上のように、最下部の[3]の一部はすでに確定しているものとします。
これについて、いつものように色分けしてみます。
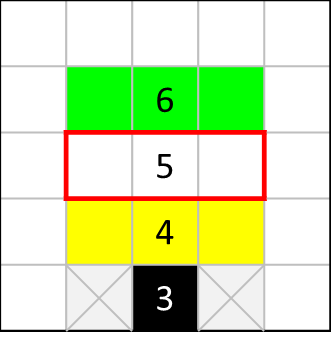
まず、[3]の視点から考えると、すでに黒マス1つが確定しており、残りは2つです。これが3つの黄色マスのうちのどれかに入ります。
次に、その上の[4]の視点から考えると、「先程の確定黒マス1つ」+「黄色マスのどこかに黒マス2つ」ですので、残り1つの黒マスが赤枠内のどこかに入ります。
さらにその上の[5]の視点から考えると、「黄色マスのどこかに黒マス2つ」+「赤枠内のどこかに黒マス1つ」と決まっているため、その上の3つの緑色マスのいずれかに黒マスが2つ入ります。
さらにさらに、その上の[6]の視点から考えると、「赤枠内のどこかに黒マス1つ」+「緑色マスのどこかに黒マス2つ」と決まっています。あと3つ、黒マスが必要なわけですが、[6]の周囲のマスも残り3つ(最上部の白マス3つ)しかありません。よって、ここがすべて黒く塗りつぶされることになります。
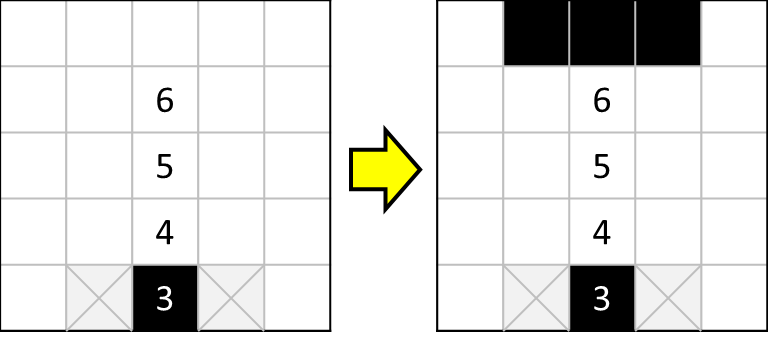
このように、1列に並んだ数字は次々と手がかりを示してくれるため、非常に重宝します。
例2

これも色分けします。
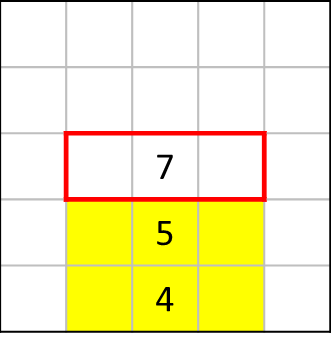
[5]の視点から見たときに、黄色マス内に4つの黒マスを配置することが確定しているため、赤枠内に入る黒マスは1つだけです。
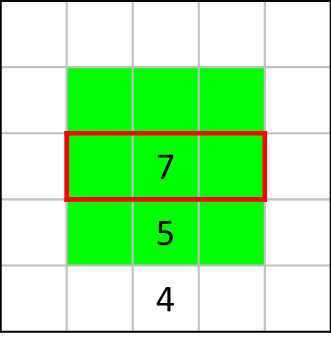
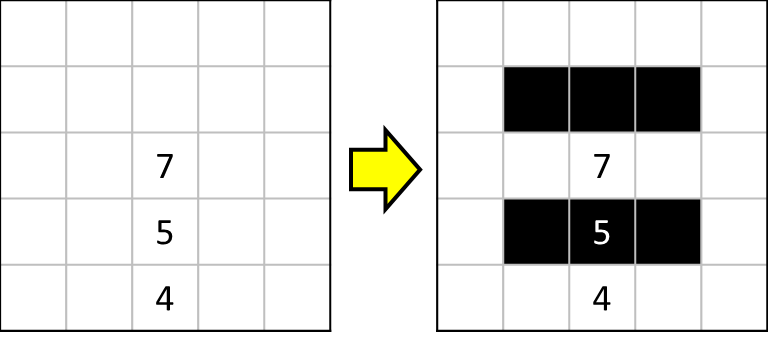
次に[7]の視点から考えると、赤枠内の黒マスが1つのみ=空欄が2つできるため、残りの部分をすべて塗りつぶさないと7つの黒マスを置くことができなくなります。
よって、[7]の周囲は赤枠内を除き、すべてを塗りつぶした以下の形になります。
例3

まずは[5]の視点から考えます。
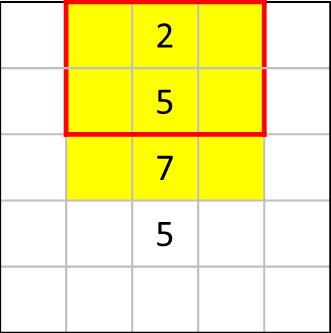
赤枠内に2つしか配置できないため、残りの3マス(赤枠外の黄色マス)をすべて黒く塗りつぶします。
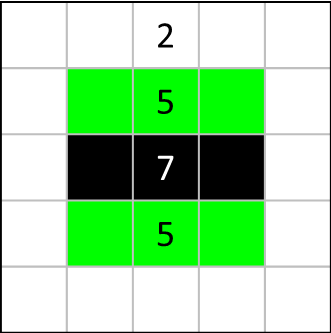
次に[7]に注目します。上図の6つの緑色マスのうち4つが黒マスになるのですが、両サイドに[5]があり、上側、下側それぞれのサイドで最大2つずつしか黒マスが置けません。そしてその最大数(上側2つ、下側2つ)を配置することでしか、[7]を満たすことはできません。
そして上下の緑色マスにそれぞれ黒マス2つを配置する場合、上下の[5]の黒マス数も同時に達成されます。つまり、それぞれの[5]の周囲のマスのうち、緑色のマス外の部分には黒マスが入らないことが分かります。
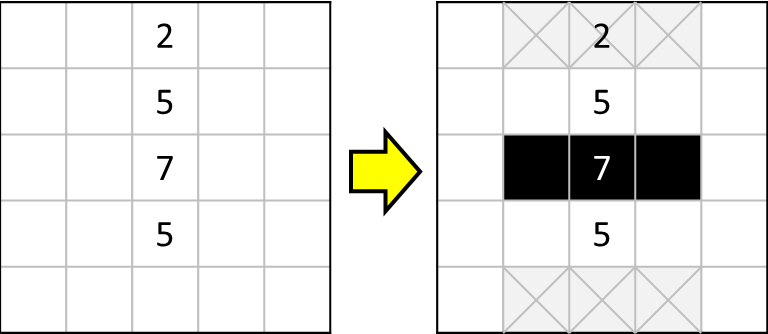
最終的には上のように、塗りつぶすマス、塗りつぶさないマスが確定します。
ここまでいくつかのパターンを紹介しましたが、最初の例に示したような、1列3マスずつに区切っていく方法は応用範囲が非常に広いです。まずはこれをしっかりマスターしておきましょう。
次は上級編②として、より複雑な形の問題を見ていきます。