3つ以上の数字の関係から解く
モザイクアート攻略のコツ~上級編①~の続きです。
ここで紹介する例は、前回のように1列に連なっているわけではありません。また、ぱっと見て「ここは解ける!」と分かるような手がかりも少ないと思います。
逆に言えば、ここで出てくるような例題が解ければ、おそらくほとんどのモザイクアートはノーヒントで最後まで解くことができるようになると思いますので、がんばりましょう。
例1

まず、[0]の周囲に×印をつけた上で、以下のように色分けします。
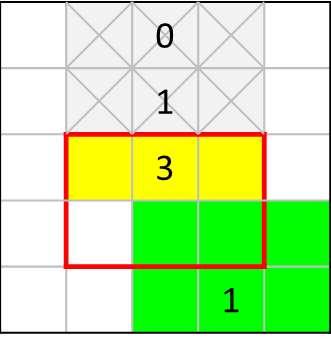
- 上の[1]の視点より、黄色マス内のどこかに黒マス1つ
- 下の[1]の視点より、赤枠内の緑色マスに最大で黒マス1つ
→赤枠内の黄色マス+緑色マスで、最大2つの黒マスとなります。
一方、赤枠内には3つの黒マスが入りますので、残った赤枠内の白マスは黒く塗りつぶされることが分かります。
また、赤枠内の緑色マスに黒マス1つを配置しておかないと[3]が成り立たなくなるので、赤枠外の緑色マスには何も入らないことになります。
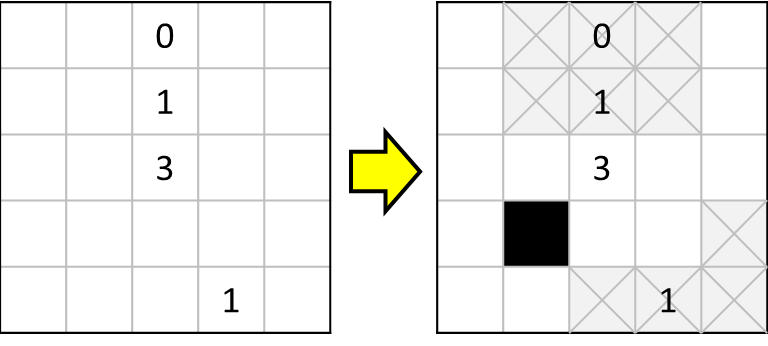
よって、上のようにいくつかのマスを確定することができます。
例2

以下のように色分けします。
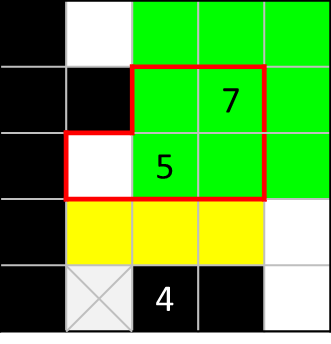
まず、[4]の黒マスは2つが確定しており、残り(黄色マス3つ)のうち2つが黒マスとなることが分かります。
次に、[5]の視点から見ると、黄色マスに2つの黒マスが入ることに加え、左上に確定黒マスが1つあるので、残りの黒マスは2つです。これが赤枠内のどこかに入ることが分かります。
最後に[7]の視点からですが、その2つの黒マスを赤枠内の緑色マスのどこかに置いたとしても、赤枠外の緑色マスはすべて塗りつぶさないと[7]が成り立ちません。
よって、赤枠外の緑色マスはすべて塗りつぶされ、かつ赤枠内の白マスには何も入らないことが分かります。
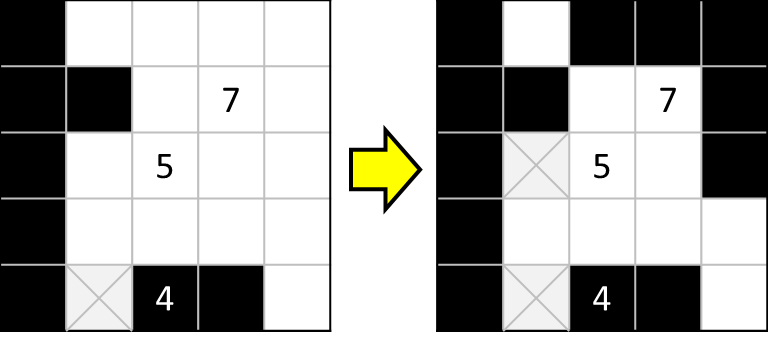
例3
これで最後です。最後にふさわしい複雑な問題、だと思います。

少し見にくいですが、[0]の周囲に×をつけた上で、以下のように色分けしました。

[4]と[5]の関係性に着目します。[5]を成立させるためには、
- 黒マスをオレンジ色マス内に1つ、赤枠内に4つ
- 黒マスをオレンジ色マス内に2つ、赤枠内に3つ
のいずれかの可能性が考えられます。この2通りの場合について[4]の視点から見ると、
- 黒マスを赤枠内に4つ、赤枠外には0
- 黒マスを赤枠内に3つ、赤枠外に1つ
となります。
一方、[6]の周囲では、残り7つのマス(緑色+青色マス)のうち、6つが黒く塗りつぶされます。つまり1マスしか空欄にできません。
しかし、上記1.の条件だと、青色マスには黒マスを配置できず、最低2つが空欄になってしまいます。よってここでは2.の条件が正解であると分かります。
このとき、[4]の赤枠外に配置される1つの黒マスは黄色マスには入らず、青色マスのどちらかに入ることになります。
(黄色マスに入れると、結局青色マスに黒マスを配置できず、[6]が成り立たなくなります)
これらにより確定するマスをまとめると、
- [5]の左側、オレンジ色のマスが黒マス確定
- [6]の周囲の緑色マスが黒マス確定
- 黄色マスは黒マスとならないことが確定
このようになります。そして、これらを盤面に落とし込んだ結果が、下のようになります。
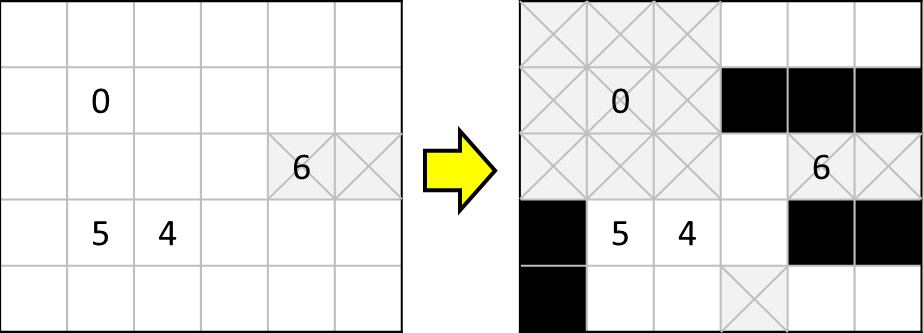
結構たくさん塗りつぶされましたね。
いかがでしたでしょうか。特に最後の例については、場合分けをする必要があるため難易度が高いですが、これぐらいまで考えることができるようになれば、解けない問題はなくなるのではないかと思います。
(将棋のように何手も先まで読む必要がない、とポジティブに捉えていただければと思います)
ここまでの内容が参考になれば嬉しいです。なかなか問題が解けないという方も、ぜひ、当ブログを参考にしつつ、ノーヒントでの攻略にチャレンジしてみてください。