前置き
モザイクアート攻略のコツ~初心者編~の続きです。
今回は、2つの数字の関わり合いから塗りつぶす/塗りつぶさないマスがいくつか確定するパターンのうち、基本的なものを見ていきます。
隣り合う3つ差の数字
次の例を見てみましょう。

まず、[7]の視点から考えます。
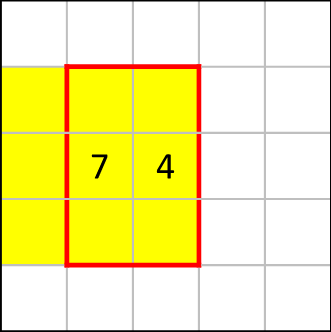
上図、9つの黄色のマス目のうち7つを黒く塗りつぶす必要がありますが、隣に[4]がある関係上、赤枠の中は最大でも4つまでしか塗りつぶすことができません。
仮にここで4つ塗りつぶしたとして、残りあと3つを塗りつぶす必要がありますが、赤枠外の黄色マスを見てみると、ちょうど3つあります。そこで、この赤枠外の黄色マスは3つとも黒く塗りつぶされることが分かります。
この[7]を成立させるためには、「赤枠外3マス(確定)」+「赤枠内4マス(6マスのうちのどれか)」を黒く塗る必要があるということです。
次に、隣の[4]の視点から考えます。
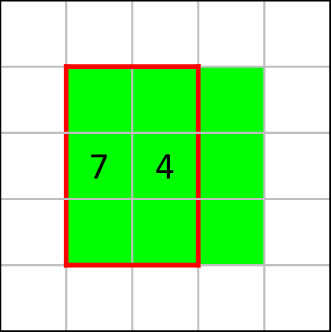
先程、赤枠の中で4つ塗りつぶされることが確定したため、残りの赤枠外の緑色マスは塗りつぶされないことが分かります。
以上をまとめると、以下のように塗りつぶされるマス、塗りつぶされないマスが確定します。
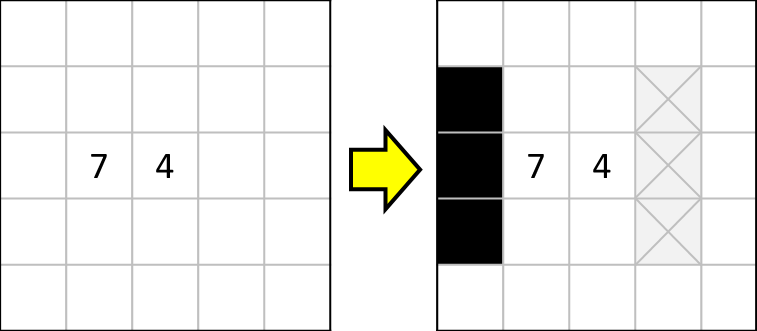
これは見出し部分に書いたとおり、隣り合う2つの数字の「差が3」のときに使える方法です。
具体的には、[1]と[4]、[2]と[5]、[3]と[6]、[4]と[7]、[5]と[8]に使えます([6]と[9]の場合は、難しく考えずに[9]を全部塗りつぶします)。
5パターンもあるので、出現頻度も比例するように高いです。
端で隣り合う2つ差の数字

先程のパターンと論理的には同じですが、隣り合う数字が端にある場合です。
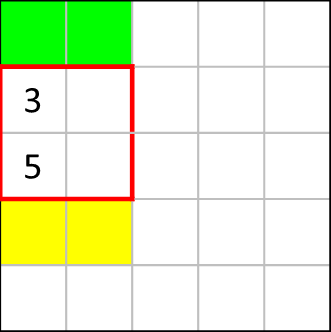
ここでも同様の考え方で、上図の赤枠内には最大3つしか黒マスを置けないため、黄色の2マスはともに塗りつぶす必要があります。また、緑色の2マスは塗りつぶしません。

パターンとしては、[1]と[3]、[2]と[4]、[3]と[5]の3パターンがあります。
斜めに隣接する5つ差の数字

これも考え方は同じですが、2つの数字の差が5と大きく、出現頻度は少し低いです。

ここでは赤枠内を3つ塗りつぶしたとしても、[8]の周辺に属する5つの黄色マスはすべて塗りつぶす必要があります。
そして5つの緑色のマスは塗りつぶすことができなくなります。
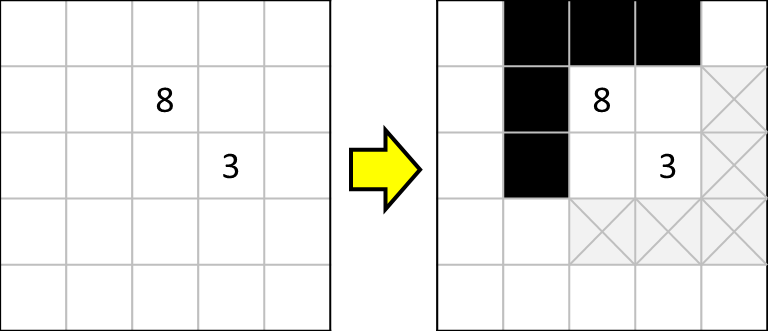
適用できるのは[1]と[6]、[2]と[7]、[3]と[8]の3パターンです。
確定できるマスが結構多いので、その分、ちょっと嬉しくなります。