前置き
ここでは、
のロジックを活用した、ちょっとした応用例を見ていきます。
例1

まずは右上の[4]を塗りつぶします。ここで、[3]の周囲を見てみると、
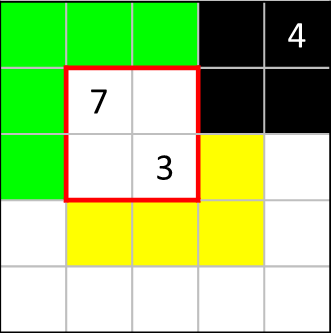
既に確定した黒マスが1つあり、残り2マスを黒く塗りつぶすことになります。
するとこの形はモザイクアート攻略のコツ~初中級者編①~の「斜めに隣接する5つ差の数字」と似た状況であることにお気づきでしょうか。
図に表すと、以下のような形に置き換えることができます。これまでに出てきたパターンに近づいた(というか、同じである)ことが分かります。
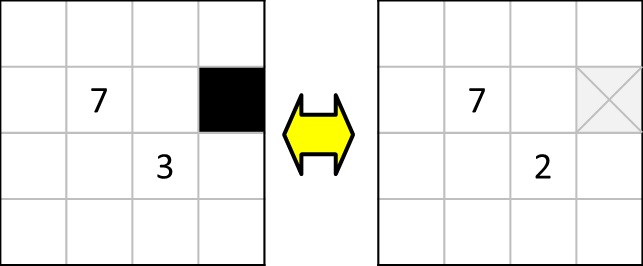
よって、以下のように塗りつぶすマス、塗りつぶさないマスを確定させることができます。
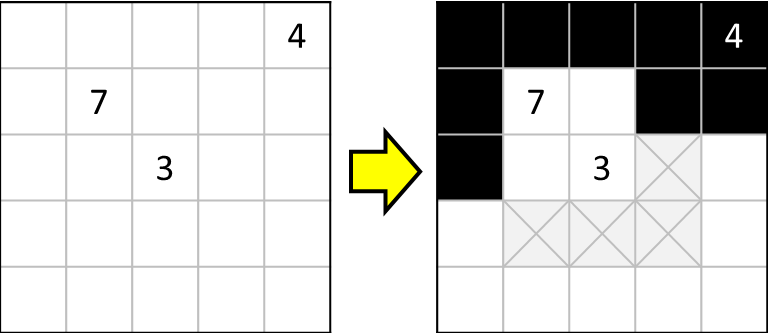
例2
例をもうひとつ。

これも結局似たような話になってしまいますが、
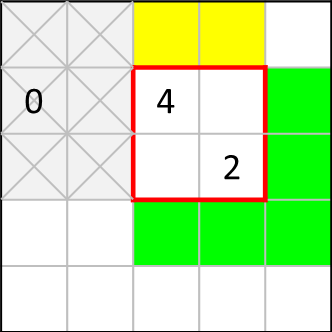
2つの数字に共通する赤枠内のマスは、最大2個までしか黒マスにできず…ということを考えると、これはモザイクアート攻略のコツ~初中級者編①~の「端で隣り合う2つ差の数字」と同じような考え方を適用でき、黄色の2マスがともに塗りつぶされることが分かります。
また、これも先程と同様に数字を置き換えて考えてみると、
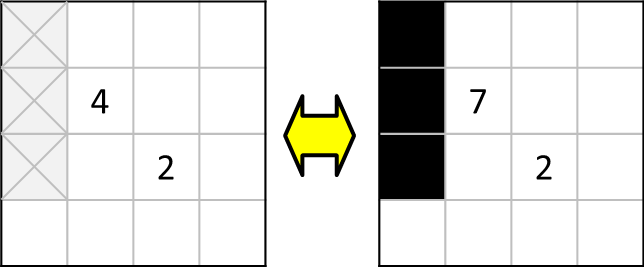
この状況とちょっと似ているわけです。こうして見ると、先程と同様、「斜めに隣接する5つ差の数字」と同パターンと考えることもできますね。
よって、以下のように塗りつぶさないマスが確定します。
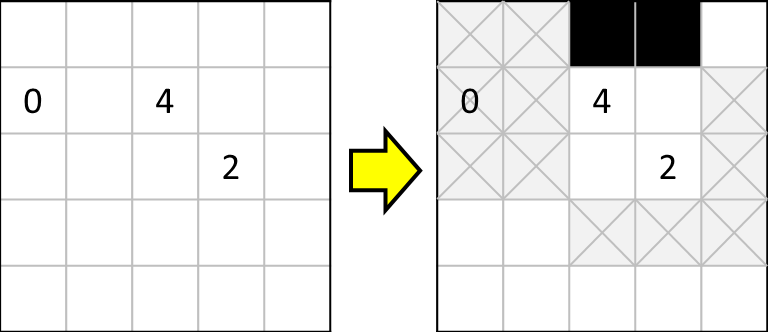
ここまでで、2つの数字の相互関係の考え方については、だいぶ慣れてきたことと思います。
次は、より実践的でパターンに当てはまらないような例について考えていきます。